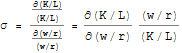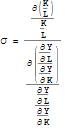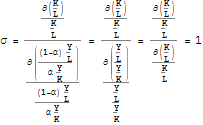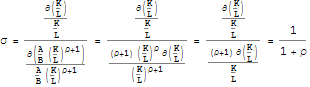|
Huub Meijers
|
|
| |
| Current page: Courses -> CES | |
|
| |
|
Last update: |
A short note on the elasticity of substitutionHuub Meijers, November 2011
In this short note I describe the elasticity of substitution between input factors as a general characteristic of production functions.For this, I use production functions in absence of technological change so the level of technology is assumed to be constant.Suppose a production function with capital (K) and labour (L) as inputs:
where Y is output (value added) and where we left out time subscripts to reduce notation.Here I use the term labour to indicate the number of workers in the production process in which I implicitly assume constant working hours per year.So the number of workers and the total number of hours worked are, besides a constant scale parameter, the same.The aggregate production function as displayed in equation (1) indicates that value added depends on two inputs: labour and capital. The number of inputs can be easily extended but for ease of exposition I use only two inputs. Specification of the functional form of (1) leads to a production function that indicates how output is related to inputs or, vice versa, how inputs relate to output. One of the main characteristics of production functions is the degree of substitution possibilities between inputs, that is: is it possible to substitute one input for another and if so, to what extent?
Before we turn to that question, some definitions: A common measure to define the degree of substitution possibilities between capital and labour is the elasticity of substitution.The elasticity of substitution (denoted by σ) of labour and capital is defined as the relative change in the capital intensity as a result of a small relative change in the ratio of the wage rate (w) and the rental rate of capital (r) for a given level of output:
If we assume competitive markets, so perfect competition on both the output and input markets, the relative factor prices should be euqal to the relative marginal products of these factors as:
such that equation (2) can be rewritten as :
If γ is equal λ to the production function f is said to describe constant returns to scale which simply says that if all inputs are increased by a certain factor, output is increased by the same factor.If γ is smaller than λ, the production function describes decreasing returns to scale whereas γ>λ indicates increasing returns to scale.
Complementary inputsInputs are said to be complementary if there are no substitution possibilities between them.This implies that for a level of output the inputs are given, independent of the relative prices of these inputs.The inputs are described by:
and it is said that in this case the input factors are complements, which implies that in order to increase the level of output, all inputs should be increased by a same relative amount. It also implies that a relative change in the wage-interest ratio does not have an effect on the labour intensity since the latter is given by :
so the elasticity of substitution (σ) is equal to zero. This function also implies that the expansion path, so all combinations of efficient use of capital and labour for given levels of output, is a straight line. This function is often referred to as the Leontief production function as it has been introduced by Wassily Leontief in Leontief, W.W., Studies in the Structure of the American Economy, Oxford, 1953. Leontief received the Nobel prize for Economics (formally the The Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel) in 1973.
Neoclassical Production Function: substitution is possibleThe Neoclassical Production function, first introduced by Robert Solow in Solow, R.M., "A Contribution to the Theory of Economic growth", Quarterly journal of Economics, LXX (1956), pp. 65 - 94, allows for substitution between labour and capital implying that, amongst others, the change in labour productivity is not only the result of technological change as in the Leontief production function, but can also be the result of relative changes in factor inputs. [This goes back to the ideas of Schumpeter (Schumpeter, J.A., Business Cycles, New York, 1939) on the separation between factor substitution and technological change]. The basic idea of the Neoclassical production function is that firms can chose between various combinations of labour and capital in order to produce the same amount of output. The basic assumptions start from a production function, like equation (1), that can be differentiated twice as:
These characteristics indicate that the Neoclassical production function exhibits positive but diminishing marginal products of labour and capital. Here we continue describing two popular Neoclassical production functions: the Cobb-Douglas and the CES production function.
Cobb - DouglasThe Cobb - Douglas is the most well known production function and is given by :
where A denotes a scale parameters which, if changing over time, can be identified with technological change. It can be easily verified that this production function is linear homogeneous, i.e. that the returns to scale is equal to one, if β = 1 - α such that the function equals:
The elasticity of substitution of the Cobb - Douglas is equal to one which can be veriified. Starting from the production function (10) and taking the marginal product of labour and capital as:
and substituting these results into (4) gives :
This indeed implies that the elasticity of substitution of the Cobb - Douglas production function is equal to 1 for all labour intensities and all capital output ratios.If β = 1 - α as assumed above the function is also linear homogeneous implying that it inhibits constant returns to scale. If α+β>1 the function represent increasing returns to scale and for α+β<1 we have decreasing returns to scale.
Constant Elasticity of Substitution (CES)The CES production function is more flexible in the sense that the elasticity of substitution is not limited to one as is the case for the Cobb - Douglas. The linear homogeneous version of the CES reads :
where the elasticity of substitution is equal to σ = 1/(1 + ρ). This can be shown as follows. The marginal product of labour divided by the marginal product of capital equals:
where we have used the fact that taking the differential of the outer function as defined by the chain rule is the same for the derivative towards labour and towards capital and thus disappears in the relative marginal products.
This also implies that the elasticity of substitution is constant throughout the entire domain of the function, hence its name. If ρ is equal to 1 the elasticity of substitution becomes one and in that case the CES function becomes equal to the Cobb - Douglas function which can be shown for ρ→0. If ρ→-1 the elasticity of substitution becomes infinite and the isoquant becomes linear as can be seen from the graphical representation of the CES production function below. For ρ→∞ the elasticity of substitution becomes zero as is the case for the Leontief production function.
Graphical example
By way of example the figure in the Wolfram CDF format that can be downloaded below presents the CES production function which is here defined as :
So A denotes a productivity factor and is bounded here to the range between 0.01 and 10. a is a share parameter defining the relative productivity of each factor of production, bounded between 0 and 1. The elasticity of substitution is here bounded between 0.01 and 5.
You can drag the sliders to see the production function changing both as three dimensional graph of labour and capital as inputs and Y as output and as isoquants as a contour plot. By clicking on the plus sign next to the slider you can see the value and have the option to let the value of that parameter go over its entire domain. Clicking on the plus sign in the right-upper corner allows to return to the initial settings. The 3-D graphs also allows to be rotated by clicking on the graph and dragging the pointer.
The interactive graph is created by using Mathematica from Wolfram using a CDF technology (Computable Document Format). The initial CDF player could be used as plug-in within all popular browsers. However, since browser support less and less plug-ins (mainly through the development of HTML5) this is not possible any more. Instead, you can download the CDF file and the stand alone CDF player that can run the CES example on a PC.
The CES production function |